AUTOCORRELATEUR SPECTAPHYSICS Model 409

AUTOCORRELATEUR SPECTRAPHYSICS Model 409

Mesurer une impulsion lumineuse de 100 fs n’est pas une simple question technique – quelle référence pouvons-nous utiliser pour mesurer un temps si court que même la lumière ne parcourt que 30 μm dans cette fenêtre ? Et puis mesurer les détails dans cette petite fenêtre ? L’une d’entre elles consiste à utiliser l’impulsion : mesurer l’impulsion par rapport à elle-même. Nous pouvons mesurer des distances (qui ne sont pas si petites ici) et utiliser la vitesse de la lumière pour convertir ces distances en temps. C’est ce qu’on appelle l’autocorrélation.

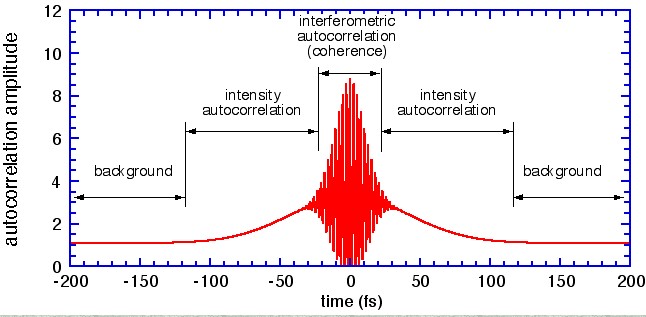
Vous pouvez facilement imaginer la forme la plus simple : un interféromètre. Si les bras de l’interféromètre ont la même longueur de trajet, il en résulte un diagramme d’interférence lorsque les faisceaux sont recombinés. Si un bras est allongé de manière à ce que les impulsions ne se chevauchent plus dans le temps lorsqu’elles se rejoignent, le motif d’interférence disparaîtra. La distance nécessaire pour sortir les copies de l’impulsion du chevauchement vous indique la durée de l’impulsion de l’impulsion.

Ce n’est pas aussi simple, cependant, à moins que l’impulsion ne soit limitée par la transformation (comme une onde porteuse avec une enveloppe gaussienne). Le motif d’inférence créé disparaîtra lorsque les copies de l’impulsion ne seront plus cohérentes les unes avec les autres, pour des distances supérieures à la longueur de cohérence des impulsions, et cela peut se produire alors que les impulsions se chevauchent encore.

Une variante meilleure que l’interférométrie simple est d’utiliser un détecteur qui mesure de manière non linéaire – par exemple, un détecteur qui ne mesure pas l’intensité I mais le carré de l’intensité. Ensuite, le signal d’une impulsion qui se chevauche ressemblera à quelque chose comme , tandis que le déplacement d’un bras de beaucoup plus que l’épaisseur d’une impulsion produira un signal qui ne se chevauche pas. Ainsi, lorsque les impulsions se chevauchent, le signal sera deux fois plus important que le signal de fond.

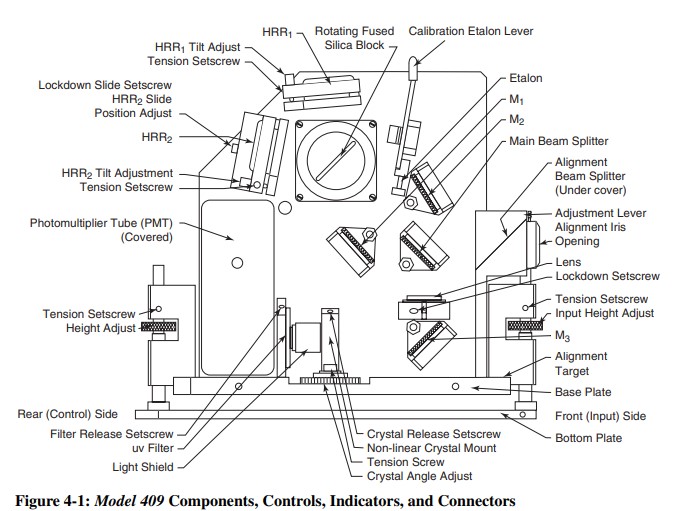
L’autocorrélateur à balayage Spectra-Physics Model 409 est un dispositif permettant de mesurer la durée des impulsions ultracourtes des systèmes laser femtoseconde (fs) et picoseconde (ps) à verrouillage de mode.L’impulsion mesurée est affichée sur un oscilloscope standard à haute impédance pour une visualisation en temps réel. Cette unité compacte ne contient que trois pièces mobiles : un bloc rotatif de silice fondue pour modifier la longueur relative du trajet optique des deux trajets de faisceau internes,un étalon qui peut être déplacé à l’intérieur et à l’extérieur de l’un de ces chemins de faisceau pour fournir un délai connu pour l’étalonnage, et un cristal de doublage qui est pour faire correspondre la phase des deux faisceaux et créer le signal d’auto-corrélation.Le modèle 409 est capable de fonctionner sur plusieurs gammes de longueurs d’onde et, en changeant les blocs rotatifs et l’étalon d’étalonnage, peut être utilisé pour mesurer des largeurs d’impulsion de 60 ps à < 40 fs.

1. Principe de base : autocorrélation optique

L’idée de l’autocorrélation optique est de comparer une impulsion ultracourte avec elle-même, en la divisant en deux copies, en introduisant un décalage temporel variable entre elles, puis en les recombinant dans un milieu non linéaire pour que l’interférence génère un signal proportionnel au recouvrement temporel des deux copies.

Voici les étapes :

Fractionnement du faisceau
Le faisceau d’impulsion incident est divisé en deux faisceaux de même intensité (via un séparateur de faisceau).
Retard optique variable
Un des faisceaux est retardé par rapport à l’autre (chemin plus long) de façon continue ou discontinue, ce qui introduit un décalage temporel $τ\tau$ .
Recombinaison dans un cristal non linéaire
Les deux faisceaux se recoupent spatialement dans un cristal non linéaire, typiquement pour faire une génération de second harmonique (SHG). Le rendement de cette génération dépend du degré de recouvrement temporel des impulsions (c’est-à-dire combien elles se superposent en temps).
Mesure de l’intensité du signal non linéaire
En mesurant l’intensité du signal (par exemple la lumière de deuxième harmonique) en fonction du retard $τ\tau$ , on obtient la fonction d’autocorrélation de l’impulsion. La forme de cette courbe permet d’inférer la durée de l’impulsion (FWHM), selon une forme d’impulsion présumée (gaussienne, sech², etc.).
Conversion du signal affiché en durée réelle
La largeur temporelle de la fonction d’autocorrélation ( $Δtac\Delta t_{\rm ac}$ ) est liée à la durée de l’impulsion $Δtp\Delta t_p$ via un facteur dépendant de la forme de l’impulsion (ex : pour une impulsion « gaussienne », $Δtp=Δtac/2\Delta t_p = \Delta t_{\rm ac} / \sqrt{2}$ , etc.). Le manuel de l’auto-corrélateur indique la relation selon les hypothèses de forme. spectra-physics.com+2Internet Archive+2

2. Spécificités du Spectra-Physics Model 409 (version 409-08)

Voici ce qu’on sait de ce modèle :

Il fonctionne selon une configuration non colinéaire (background-free), ce qui signifie que les deux faisceaux ne sont pas strictement alignés sur le même axe, ce qui permet d’éliminer le bruit de fond dû à la SHG des faisceaux individuels. spectra-physics.com
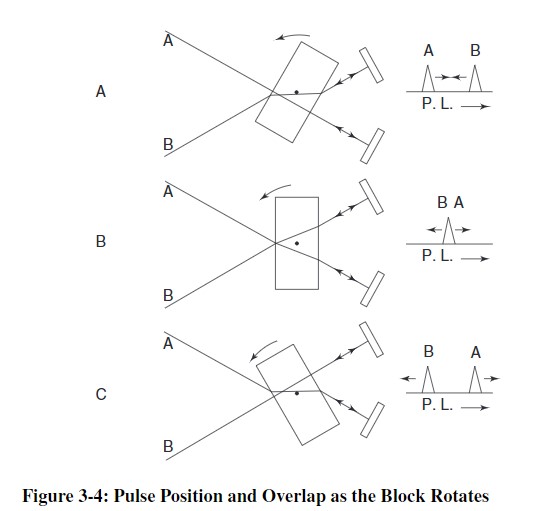
Il utilise un bloc tournant en silice fondue pour créer le retard variable entre les deux bras optiques. Le déplacement (rotation) de ce bloc modifie le chemin optique différentiel. spectra-physics.com+2spectra-physics.com+2
Le système est calibré à l’aide d’un étalon (étalon calibré) insérable dans un des bras pour ajuster la base de temps du balayage du retard. spectra-physics.com+2spectra-physics.com+2
La plage de longueurs d’onde utilisable est environ 650 à 1600 nm (selon les cristaux disponibles) pour ce modèle. spectra-physics.com+1
En changeant les blocs tournants (épaisseur différente), on peut couvrir des durées d’impulsion allant de l’ordre de 25 ps jusqu’à < 80 fs selon la configuration. spectra-physics.com+1
Le manuel du 409 mentionne que, comme pour tout autocorrélateur, l’impulsion subit un certain élargissement à l’intérieur de l’instrument (dispersion optique), donc une correction (compensation de dispersion) est nécessaire pour les impulsions très courtes afin d’estimer la durée réelle. spectra-physics.com+2spectra-physics.com+2
Le manuel complet de ce modèle est disponible (texte complet) sur Archive.org, ce qui permet de voir les instructions exactes de nettoyage, d’alignement, etc.

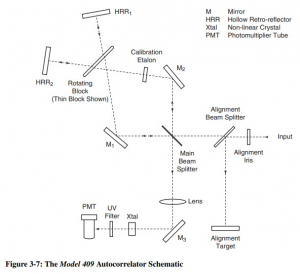
3. Fonctionnement optique – chemin optique (schéma simplifié)

Voici un schéma conceptuel :

Le bloc tournant modifie le chemin optique différentiel entre les bras A et B.
Le cristal non linéaire (ex : un cristal de SHG) convertit l’interaction des deux impulsions en lumière à une fréquence doublée, uniquement si elles coïncident dans le temps.
Un filtre optique permet de sélectionner la lumière de seconde harmonique (et rejeter la lumière fondamentale).
Le détecteur (souvent un photomultiplicateur ou un photodétecteur sensible aux UV) mesure l’intensité de la lumière SHG, donnant un profil en fonction du retard.

Dans la configuration background-free, le signal de SHG dû aux impulsions individuelles ne contribue pas dans la même direction spatiale que le signal de combinaison, ce qui permet d’éviter un fond constant et augmente la sensibilité du signal d’autocorrélation. spectra-physics.com

4. Calcul de la durée de l’impulsion

Après avoir obtenu la courbe d’autocorrélation (intensité SHG vs retard $τ\tau$ ), il faut :

Mesurer la largeur à mi-hauteur (FWHM) du pic d’autocorrélation, $Δtac\Delta t_{ac}$ .
Appliquer le facteur de conversion selon l’hypothèse de la forme de l’impulsion (gaussienne, sech², etc.). Par exemple, pour une impulsion gaussienne, $Δtp=Δtac/2\Delta t_p = \Delta t_{ac} / \sqrt{2}$ . Pour une impulsion “sech²”, $Δtp≈Δtac/1.543\Delta t_p ≈ \Delta t_{ac} / 1.543$ , etc. Le manuel du 409 donne les facteurs de conversion. spectra-physics.com+1
Corriger l’élargissement dû à la dispersion optique dans l’autocorrélateur lui-même (et dans l’ensemble optique), pour les impulsions très courtes.

Il est donc important que le système optique jusqu’à l’autocorrélateur (lenses, fenêtres, cristaux, etc.) soit bien calibré ou compensé en dispersion.

5. Limitations et précautions

Pour des impulsions très courtes (quelques dizaines de fs), la dispersion (GVD) due aux éléments optiques dans l’autocorrélateur (et dans les optiques externes) peut être non négligeable — il faut la compenser ou au moins la connaître. spectra-physics.com+1
L’alignement optique doit être précis : le recouvrement spatial et temporel des impulsions dans le cristal est crucial.
Le détecteur doit être suffisamment sensible et linéaire, et le signal ne doit pas saturer l’autocorrélateur.
Le nettoyage des optiques internes est délicat : le manuel du 409 donne des instructions pour le nettoyage et la manipulation sans endommager les surfaces fragiles.
Le modèle a une plage opérationnelle en longueur d’onde et en durée d’impulsion, au-delà de laquelle les performances chutent ou l’instrument n’est plus adapté