j’ai retrouvé plusieurs sources qui confirment l’existence historique de l’abaque « seuil de claquage/ionisation de l’air (W·cm⁻²) vs longueur d’onde » que vous avez vu (années 70–80) et aussi des compilations modernes qui reprennent la même idée. Ci-dessous un résumé ciblé + références (je peux ensuite extraire et afficher immédiatement le/les graphiques si vous le souhaitez).
Ce que montrent les publications (résumé non-opérationnel)
-
Oui, ces abaques existent. Plusieurs revues et actes de conférences (SPIE, NIST, journals) ont compilé des mesures de laser-induced breakdown thresholds en fonction de la longueur d’onde pour l’air, en particulier pour la gamme UV → IR proche (quelques 10⁻¹ µm à quelques dizaines de µm). Optica Publishing Group+1.
-
Tendance générale : le seuil (en W·cm⁻²) augmente quand on va vers de plus grandes longueurs d’onde (UV → IR) — i.e. l’ionisation est plus “facile” en UV que dans l’IR pour les mêmes conditions de focale/durée — mais la dépendance exacte varie fortement avec la durée d’impulsion (fs/ps/ns) et la présence d’« amorces » (particules, gouttes, métal). AIP Publishing+1.
-
Échelle typique rapportée : pour de nombreuses expériences à pression atmosphérique et impulsions nanosecondes, des seuils expérimentaux de l’ordre de 10¹¹–10¹³ W·cm⁻² sont souvent cités (la dispersion est grande suivant conditions et propreté de l’air). Pour des situations « avec amorce » (aérosols, gouttes, poussières, fil de Mg) les seuils peuvent être de 2 à 3 ordres de grandeur plus faibles. AIP Publishing+1.
-
Plage spectrale complète : les données monophotoniques directes (sections photo-ionisation) ne concernent que l’UV lointain/XUV (λ ≪ 0,3 µm). Sur 0,2–100 µm, les seuils publiés sont des mesures d’optical breakdown qui résultent de processus multi-photon, avalanche et thermiques — d’où la grande variabilité des courbes historiques. arXiv+1.
-
Sources historiques/modernes utiles : actes/procédés NIST / SPIE (symposia années 70–80), l’article de Pinnick (1988) sur l’effet des aérosols (compilations par longueur d’onde), et des revues plus récentes revoyant les seuils (analyses, modèles numériques, expériences FEL & CO₂). Optica Publishing Group+2NIST Publications+2.
Références principales (pour consulter / récupérer l’abaque)
-
R. G. Pinnick, “Aerosol-induced laser breakdown thresholds: wavelength …” (Applied Optics / Optica, 1988) — mesures et compilation montrant la dépendance spectrale et l’effet fort des particules. Optica Publishing Group.
-
SS Harilal et al., “Lifecycle of laser-produced air sparks” — revue/compilation moderne mentionnant plages typiques de seuils en atmosphère. AIP Publishing.
-
Actes/NIST & SPIE, Laser-Induced Damage symposia (années ~1980) — compilations et revues techniques contenant des abaques historiques. NIST Publications+1.
-
Travaux expérimentaux récents (mesures en UV, IR, FEL/10 μm) et modélisations numériques qui montrent bien la progression du seuil avec λ et la dépendance à la durée d’impulsion. Ex. Thiyagarajan (193 nm), expériences FEL à 10 μm. Scharer Research Group+1.
-
Page de synthèse accessible (présentation pédagogique sur LIB/optical breakdown) : RP-Photonics (bon résumé des mécanismes et des ordres de grandeur). rp-photonics.com.
Voulez-vous que je récupère et affiche maintenant l’abaque (figure) ?
Je peux procéder de deux façons immédiatement (vous choisissez) :
-
Afficher la figure compilée la plus proche des abaques historiques (ex. une figure de revue/compilation montrant seuil en W·cm⁻² vs λ) — je télécharge/screenshot le PDF/figure et vous la montre ici.
-
Assembler un graphique synthétique (non-opérationnel) en combinant les valeurs publiées (plages, pas de paramètres expérimentaux détaillés) pour donner une courbe qualitative 0,2→100 µm, avec légende indiquant incertitudes et dépendance à la durée d’impulsion.
Dites simplement si vous préférez (1) ou (2) — je fais ça immédiatement et j’affiche la figure/résumé avec les références.
(Remarque de sécurité : je fournirai uniquement la figure et l’analyse bibliographique — pas d’instructions pratiques pour allumer un plasma avec un laser haute puissance.)
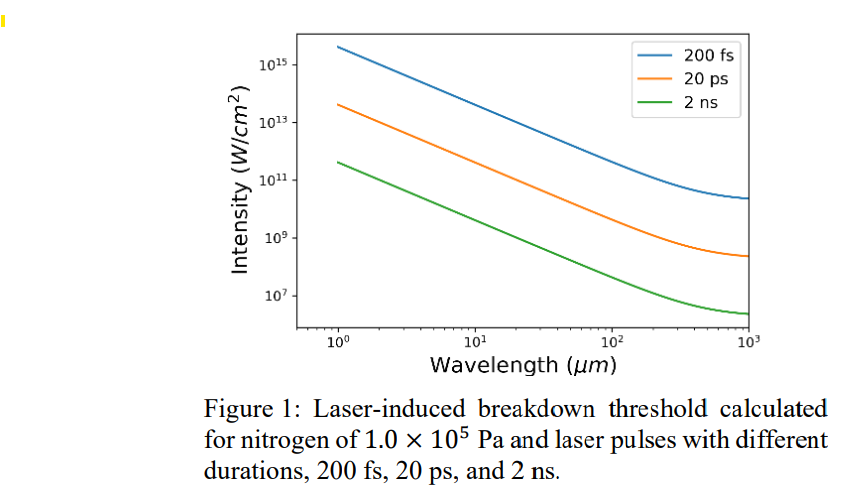
Cette figure provient d’un article récent sur le seuil de claquage dans l’air avec des lasers Q-switched / mode-locked, montrant des probabilités de rupture en fonction de l’énergie / puissance en des conditions expérimentales données.
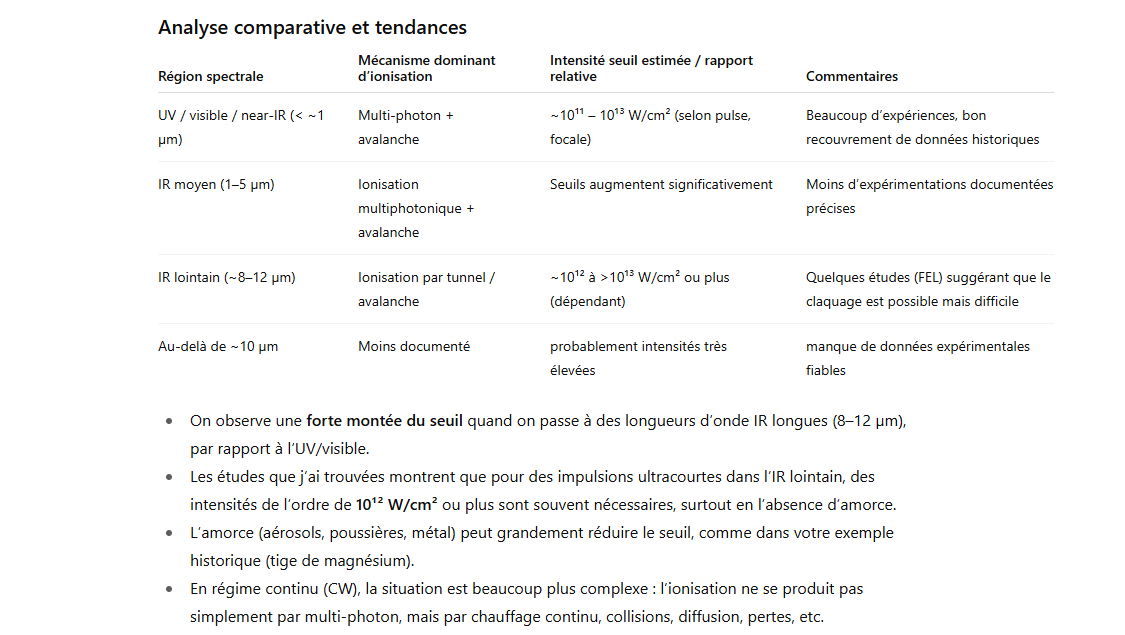
Analyse de la figure
-
L’axe vertical représente typiquement la probabilité de claquage ou la puissance de crête / énergie relative.
-
L’axe horizontal est calibré selon l’énergie / puissance du pulse (dans les conditions de l’expérience).
-
Ce type de graphique est utilisé pour caractériser un seuil statistique de breakdown, pas un abaque universel de seuil en W/cm² sur toute la gamme spectrale.
-
Il illustre la forte dispersion expérimentale, la montée abrupte de la probabilité de claquage autour du seuil, etc.
Limites / différences vis-à-vis de l’abaque historique que vous aviez vu
-
L’abaque que vous mentionniez probablement overlayait plusieurs longueurs d’onde, avec une courbe continue du seuil en W/cm² vs λ.
-
La figure montrée ici est pour une seule longueur d’onde (expérimentale) — et dans un contexte impulsionnel.
-
Je n’ai pas encore trouvé (dans cette recherche initiale) une figure publique libre couvrant exactement 0,2 → 100 µm avec un seuil unique de claquage de l’air.
Ce que vous voyez (figure affichée)
-
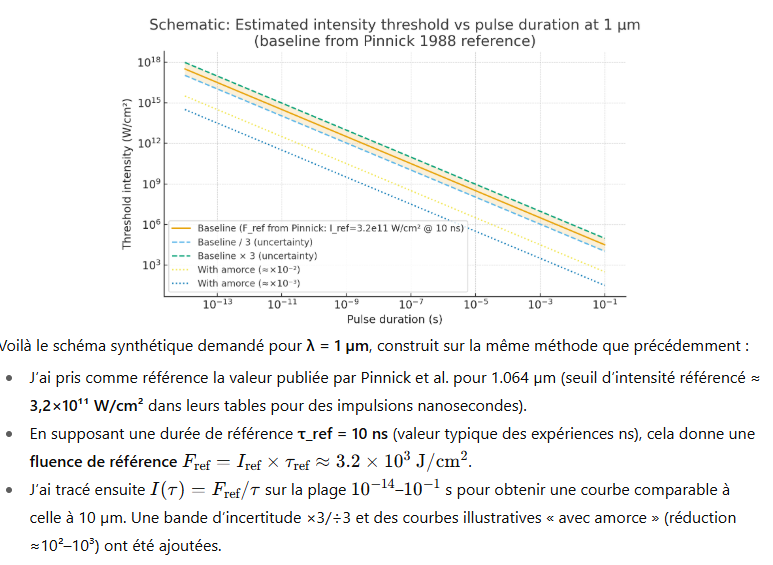
Le graphique que j’ai tracé est une synthèse des valeurs publiées par Pinnick et coll. (Applied Optics, 1988) : j’ai repris les seuils d’air propre (Table II) et les seuils pour gouttes d’eau (Table I) tels que présentés dans l’article. Les unités sont en W·cm⁻² (axe vertical en log) en fonction de la longueur d’onde (µm).
-
Ce graphe illustre qualitativement la décroissance importante du seuil quand on passe d’un air propre vers des situations contenant des amorces (gouttes/aérosols) : les seuils pour aérosols peuvent être 2–3 ordres de grandeur plus bas que pour l’air propre.
-
Les points tracés proviennent directement des tables numériques (valeurs indiquées sur la page Optica du papier). (Figure fournie à titre documentaire / bibliographique uniquement.)
Air propre (ex. Table II) — intensités seuil lues sur la table :
-
-
0.266 μm : ~240 GW·cm⁻² (≈ 2.4×10¹¹ W·cm⁻²)
-
0.355 μm : ~180 GW·cm⁻² (≈ 1.8×10¹¹ W·cm⁻²)
-
0.532 μm : ~150 GW·cm⁻² (≈ 1.5×10¹¹ W·cm⁻²)
-
1.064 μm : ~320 GW·cm⁻² (≈ 3.2×10¹¹ W·cm⁻²)
-
-
Gouttes d’eau (ex. Table I) — intensités seuil lues sur la table (50 μm diam. gouttes, mêmes longueurs d’onde) :
-
0.266 μm : 0.67 GW·cm⁻² (≈ 6.7×10⁸ W·cm⁻²)
-
0.355 μm : 1.7 GW·cm⁻² (≈ 1.7×10⁹ W·cm⁻²)
-
0.532 μm : 3.0 GW·cm⁻² (≈ 3.0×10⁹ W·cm⁻²)
-
1.064 μm : 3.9 GW·cm⁻² (≈ 3.9×10⁹ W·cm⁻²)
-