Mesure de la durée de pulse femtoseconde par auto-corrélation.
Principe général de l’autocorrélation optique
-
Les impulsions femtosecondes sont trop brèves pour être mesurées directement par les détecteurs électroniques classiques.
-
La solution est de caractériser la durée du pulse en utilisant un processus non linéaire (dépendant de l’intensité), déclenché uniquement lorsque deux portions du pulse se recouvrent temporellement.
-
L’autocorrélateur FR103XL exploite ce principe en divisant le pulse, en introduisant un retard variable entre les deux répliques, puis en mesurant la réponse non linéaire issue de leur recouvrement.
-
Les étapes clés de la mesure
a) Séparation du faisceau
-
Une lame séparatrice (beam splitter) divise l’impulsion incidente en deux bras.
-
Ces deux pulses suivent des trajets optiques légèrement différents.
-
L’un des bras passe par un retard variable (généralement monté sur un miroir mobile), ce qui permet de contrôler le décalage temporel entre les deux pulses.
b) Recouvrement spatial et temporel
-
Les deux pulses recombinés sont focalisés dans une zone non linéaire.
-
Selon la configuration de l’autocorrélateur, cette interaction peut se faire dans :
-
un cristal non linéaire (par ex. BBO) pour générer la seconde harmonique (SHG), ou
-
un détecteur basé sur l’absorption à deux photons dans un semi-conducteur (par ex. GaAs, Si photodiode spéciale).
-
Détection non linéaire
- Autocorrélation par génération de seconde harmonique (SHG)
-
Lorsque les deux pulses se recouvrent temporellement, leur intensité combinée est suffisante pour générer une lumière à la fréquence doublée (2ω).
-
L’intensité de la SHG mesurée en fonction du retard donne la courbe d’autocorrélation.
-
-
Autocorrélation par absorption à deux photons
-
Le semi-conducteur absorbe deux photons simultanément seulement quand les pulses se chevauchent temporellement.
-
Le signal détecté est proportionnel à l’intensité croisée des deux pulses → permet aussi de tracer la fonction d’autocorrélation.
-
d) Tracé et interprétation
-
Le détecteur enregistre l’intensité du signal non linéaire en fonction du retard introduit.
-
On obtient une courbe d’autocorrélation :
-
Largeur du pic → durée de l’impulsion.
-
La forme (gaussienne, sech², etc.) permet d’extraire la durée réelle via un facteur de correction (≈ 0.707 pour Gauss, ≈ 0.648 pour sech²).
-
Points importants pour réussir la mesure
-
Alignement précis : les deux bras doivent parfaitement se recouvrir spatialement dans le cristal ou sur le détecteur.
-
Dispersion minimale : éviter d’introduire du verre épais, qui allonge artificiellement l’impulsion.
-
Choix du mode (SHG vs absorption 2 photons) :
-
SHG = signal plus fort, mais nécessite un cristal adapté à la longueur d’onde.
-
Absorption 2 photons = plus simple (pas besoin de phase-matching), mais signal souvent plus faible.
-
-
Calibration du retard : indispensable pour convertir la largeur du signal en femtosecondes réelles.
-
Type d’impulsion : le FR103XL mesure la durée mais pas la phase → il ne fournit pas le profil exact du pulse, seulement une estimation de la largeur temporelle.
-
-
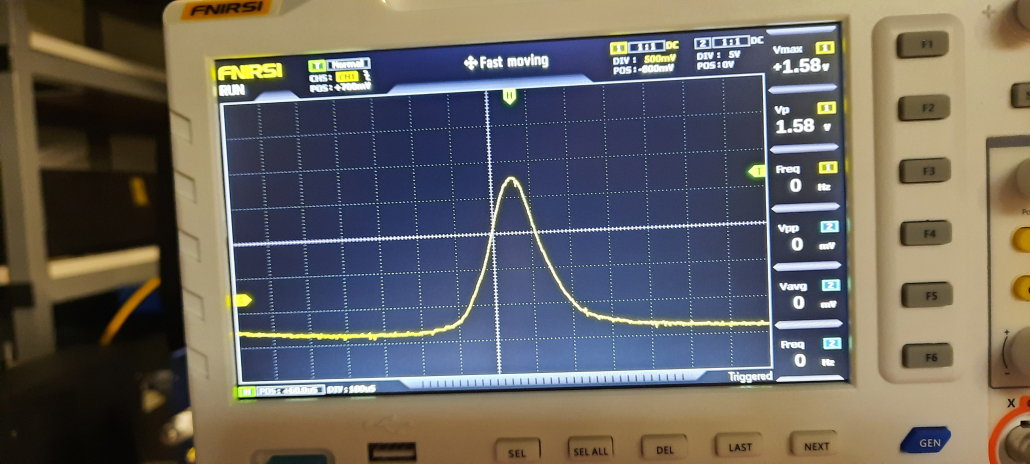
Mesure de la durée de pulse avec un auto-corrélateur FEMTOCHROME Model FR103XL d’une résolution de 1 fs!
La mesure est effectuée sur un laser Yb:KGW ORIGAMI 10 de la société ONE FIVE et sur un laser fibré Yb:SiO2 de la société AMPLITUDE SYSTEMS
Résultat des mesures sont 130 us pour le laser AMPLITUDE SYSTEMS soit 133 fs et 200 us pour le laser ORIGAMI 10 soit 205 fs.
https://chatgpt.com/c/68d45fee-7b40-8332-947c-ba589d6f2d01
L’auto-corrélateur se compose d’une lame séparatrice de 1 micron d’épaisseur sur laquelle le faisceau à analyser est divisé en 2 parts.
Une part est dirigée dans un bras fixe et l’autre part est dirigée dans un bras muni de 2 miroirs tournant autour d’un axe à 10 tours par seconde et renvoyé par le miroir M3 sur le miroir M2.
Ce bras varie de longueur 20 fois par seconde.
Le faisceau issue du bras fixe est renvoyé sur le miroir M2. Le miroir M2 concave focalise les 2 faisceaux sur un cristal doubleur de fréquence.
Le faisceau doublé en fréquence entre par un orifice de 0.5mm sur un photomultiplicateur. Le gain est réglé par la tension d’alimentation entre 100 volts et 1000 volts.
Avec une fréquence de rotation de 10Hz l’affichage sur l’oscilloscope est de 1.46ps/ms
Pour un pulse de forme Gaussien le coefficient est de 0.707
Lame séparatrice — quel type pour éviter l’étirage temporel?
Objectif : minimiser la quantité de verre traversée (donc la dispersion de groupe — GVD / GDD) tout en conservant une bonne stabilité mécanique et un ratio réflexion/transmission adapté.
Options (classement conseillé pour 5 fs) :
-
Pellicle beam-splitter (pellicule) — préférence n°1 pour 5 fs
-
Épaisseur typique : quelques micromètres (1–3 μm).
-
Avantage : quasi-négligeable en terme de dispersion (pratiquement pas de GDD ajouté), donc idéal pour impulsions de quelques fs.
-
Inconvénients : fragile, limité en diamètre utile et en seuil d’endommagement, peut avoir des inhomogénéités et produire des franges d’interférence si polarisation non contrôlée.
-
Usage : si faisceau de petite section et environnement contrôlé, c’est le meilleur choix.
-
-
Cube ou plate en verre à film mince (fused-silica, thin film BS) — solution secondaire
-
Épaisseur minimale réalisable pour une plaque en verre : typiquement ≥ 0.1 mm (100 µm) pour des plaques industrielles ; cubes plus épais (mm).
-
Avantage : robuste, bonne stabilité mécanique, haut seuil d’endommagement.
-
Inconvénient : introduit GVD/GDD proportionnel à l’épaisseur — attention pour 5 fs.
-
Si on doit utiliser du verre, privilégier fused silica (faible dispersion relative) avec coatings à large bande et la plus petite épaisseur possible. Éviter les adhésifs intercalés (colles) si possible.
-
-
Beam-splitter polariseur + lame de retard (Brewster / polarizing cube)
-
Peut être utile selon la polarisation du laser, mais souvent implique davantage de verre ou optiques auxiliaires → pas optimal pour 5 fs sauf si conçu avec des composants ultraminces.
-
Chiffres utiles (ordre de grandeur)
-
GVD (fused silica) ≈ 36 fs²/mm autour de 800 nm (valeur indicative).
-
Une plaque de 0.1 mm (100 µm) ajoute ≈ 3.6 fs² de GDD.
-
Une plaque de 1 mm ajoute ≈ 36 fs².
Pour des impulsions de 5 fs, même quelques fs² de GDD commencent à être non négligeables (chirp, léger allongement). D’où l’intérêt fort d’une pellicule.
-
Recommandation résumée :
-
Si possible → pellicle (1–3 µm).
-
Sinon → fused-silica thin plate la plus mince possible, avec coatings larges bande et compensez la dispersion (voir section compensation).
2) Cristal doubleur (SHG) — quelle épaisseur pour 5 fs ?
Objectif : obtenir un signal SHG suffisamment intense tout en préservant une bande passante large (pour ne pas tronquer le spectre du pulse) et en limitant le group-velocity mismatch (GVM).
Considérations physiques :
-
Plus le cristal est épais → meilleure conversion SHG (signal ↑) mais → réduction de la bande passante utile et augmentation du GVM (les fréquences différentes glissent temporellement).
-
Pour impulsions ultrabrèves (quelques fs) il faut favoriser cristaux très fins pour garder la large bande spectrale.
Matériaux courants et recommandations :
-
BBO (β-BaB₂O₄), Type I — le plus utilisé pour SHG ultrabroadband (longueurs d’onde ~700–1000 nm).
-
Épaisseur recommandée pour 5 fs : ≈ 5–20 µm.
-
Pratique courante : 10 µm est un bon compromis conversion / bande passante.
-
Avantages : large bande passante de phase-matching, bonne résistance optique.
-
Remarque : manipulation et montage délicat pour épaisseurs < 20 µm ; attention au polissage et revêtements AR.
-
-
KD*P, LiB3O5 (LBO) etc. → généralement moins favorables pour impulsions < 10 fs à cause de bande passante de phase-matching plus limitée ou GVM plus élevé. BBO reste préféré.
Autres points :
-
Couplage non colinéaire (noncollinear SHG) : permet d’élargir la bande passante effective — souvent utilisé dans les autocorrélateurs pour fs courts.
-
Revêtements AR sur le cristal et angle de coupe optimisés pour la longueur d’onde centrale.
-
Éviter épaisseurs >~50 µm pour 5 fs : trop de filtrage spectral et GVM → allongement net du signal d’autocorrélation.
3) Stratégies complémentaires à adopter
-
Minimiser tout verre additionnel (lentilles, fenêtres, filtres) dans les bras ; préférer miroirs réfléchissants à large bande plutôt que lentilles en transmission.
-
Compensation de dispersion : même en prenant pellicle + cristal ultrafin, il est souvent nécessaire d’équilibrer la dispersion résiduelle (miroirs chirpés, paires de prismes, ou compenseur en verre) pour retrouver un pulse le plus court possible dans la zone de SHG.
-
Focalisation : utiliser une focale raisonnable (éviter focales trop courtes qui provoquent SPM ou ionisation) ; pour SHG dans une fine BBO, on emploie souvent une mise au point modérée afin d’augmenter l’intensité sans étendre le spectre par SPM.
-
Polarisation : contrôler strictement la polarisation pour optimiser le SHG (Type I exige polarisation définie).
-
Calibration : connaître précisément la longueur d’onde centrale et la bande spectrale de ton laser — cela conditionne le choix exact du cristal (angle de coupe) et des coatings.
-
BBO (10 µm) : la dispersion (GVD) de la BBO à 1030 nm conduit à un GDD ≈ 0.42 fs² pour 10 μm — effet négligeable sur une impulsion de 5 fs (largeur FWHM passe ~ 5.00 → 5.005 fs). refractiveindex.info
-
Feuille d’or 2 μm : inadéquate — l’or est un métal fortement absorbant (skin-depth ~ 20–45 nm dans le proche IR). Une couche de 2 µm est donc pratiquement totalement opaque (transmission ≈ exp(−2000 nm / 30 nm) ≈ 10⁻²⁸), provoque une perte énorme et risque d’altérer/absorber l’impulsion plutôt que de la diviser proprement. Ne pas utiliser une feuille d’or de 2 µm comme beamsplitter pour des pulses de quelques fs.
-
Calculs détaillés (méthode + valeurs)
1) Dispersion de la BBO (Sellmeier)
J’ai utilisé la formule Sellmeier pour la BBO (Eimerl) disponible dans la base RefractiveIndex.info :
n2(λ)=2.7405+0.0184λ2−0.0179−0.0155λ2n^2(\lambda)=2.7405 + \dfrac{0.0184}{\lambda^2 – 0.0179} – 0.0155\lambda^2 avec λ\lambda en µm. refractiveindex.infoÀ partir de là j’ai calculé numériquement la d²n/dλ² à λ = 1030 nm, puis utilisé la relation standard (convertie en unités pratiques) pour obtenir la GVD (β₂) en fs²/mm :
GVDBBO(1030 nm)≈42 fs2/mm\text{GVD}_{\text{BBO}}(1030\ \text{nm}) \approx 42\ \text{fs}^2/\text{mm}
-
Pour une épaisseur de 10 μm = 0.01 mm :
GDD=GVD×eˊpaisseur≈42 fs2mm×0.01 mm≈0.42 fs2.\text{GDD} = \text{GVD}\times \text{épaisseur} \approx 42\ \frac{\text{fs}^2}{\text{mm}}\times 0.01\ \text{mm} \approx 0.42\ \text{fs}^2.
2) Impact sur une impulsion de 5 fs (Gaussian, FWHM)
Pour une impulsion gaussienne d’entrée τ₀ = 5 fs (FWHM) on convertit en écart-type temporel σ=τFWHM/2.3548\sigma=\tau_{FWHM}/2.3548. L’expression (voir encyclopédies / RP Photonics) donne la largeur après propagation dans un élément avec GDD total = DD :
σpost=σ2+(D2σ)2\sigma_\text{post}=\sqrt{\sigma^2 + \left(\dfrac{D}{2\sigma}\right)^2}
En utilisant D=0.42 fs2D = 0.42\ \text{fs}^2 on trouve :
-
σ_before ≈ 2.123 fs → τ_FWHM_before = 5.00 fs
-
τ_FWHM_after ≈ 5.005 fs
Conclusion : allongement négligeable (≈ +0.005 fs) dû au seul BBO de 10 μm.
3) Feuille d’or 2 μm — pourquoi c’est mauvais
-
Skin depth (optical penetration) de l’or dans le near-IR est typiquement de l’ordre de 20–45 nm (voir Olmon et al. et bases de données optiques). Une feuille de 2000 nm dépasse largement la skin depth. Physical Review+1
-
Transmission approximative (modèle exponentiel) : T∼e−t/δT \sim e^{-t/\delta}. Avec δ ≈ 30 nm et t = 2000 nm → T∼e−66.7∼10−29T \sim e^{-66.7} \sim 10^{-29}. En pratique : zéro transmission utile; l’armé «transmise» serait quasi nulle, l’autre bras fortement modifié par absorption thermique/plasmonique.
-
Même en réflexion : un miroir d’or épais impose pertes d’absorption, modifications spectrales (absorption & phase), et peut introduire une dispersion complexe — mais en tout cas ce n’est pas adapté pour splitter en deux pulses de femtoseconde sans dégradation.
-
https://www.manualslib.com/products/Femtochrome-Fr-103mn-8670747.html
Manuel d’utilisation de l’auto-correlateur FR103XL